 問題を解くという行為は、一人森の中に残され、そこからゴールを目指す事に似ています。その森が幸運にも以前来た事のある森ならばゴールまでの道筋を覚えている事もあるかもしれません。しかし、多くの場合はその森は初めて迷い込んだ森であり、そんな時、過去の「記憶」は頼りになりません。けれども、もし迷ったその人が地図と磁石を持つならば、どのような森であってもその2つを駆使してきっとゴールにたどり着くことができるでしょう。
問題を解くという行為は、一人森の中に残され、そこからゴールを目指す事に似ています。その森が幸運にも以前来た事のある森ならばゴールまでの道筋を覚えている事もあるかもしれません。しかし、多くの場合はその森は初めて迷い込んだ森であり、そんな時、過去の「記憶」は頼りになりません。けれども、もし迷ったその人が地図と磁石を持つならば、どのような森であってもその2つを駆使してきっとゴールにたどり着くことができるでしょう。
勉強において「地図と磁石」を持てる人間は、新しい問題にあたった時に第一歩を自信をもって正しい方向に踏み出すことができます。テストで問題用紙をめくる時、以前やったことのある問題であることを祈るより、この「地図と磁石」を持てるようになることを目指す方がずっとずっと本質的でそして楽しいとは思いませんか?
では、具体的には「地図と磁石」とはどのようなものでしょうか?
ここに簡単な例を一つ出します。
問題
「1から10まですべて足し合わせるといくつになるか答えなさい」
解:55
もちろん地道に計算をしてもすぐに答えは出ます。中には答えを暗記している人もいるかも知れません。等差数列の和の公式を覚えていて
$$ \frac{(初項+末項) \times 項数 }{2}= \frac{(1+10) \times 10}{2}=55$$
と計算した人もいるでしょう。しかし、このどれもがこの場合の「地図と磁石」ではないのです。 この場合の「地図と磁石」は、
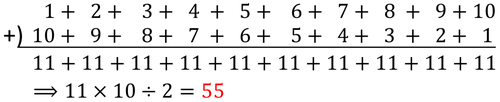
のように、考えることです。
これを少し進めて考えれば先の「等差数列の和の公式」へとすぐにたどり着きます。
この「地図と磁石」を持たないで、ただ公式として「等差数列の和の公式」を丸暗記している(していた)人は、少し応用問題を出されただけで途端にできなくなってしまったり、そもそも公式そのものを間違って覚えてしまっていたり、あるいはすっかり忘れてしまっていたりする事が少なくありません。しかし、この「地図と磁石」を持っている人は、この考え方を使って解ける問題の多いことに驚くでしょうし、公式はもはや知識ではなく知恵として一生忘れない財産になります。
まさにここに「地図と磁石」を手に入れるためのヒントとその醍醐味があります。
上の例で「逆に並べて上下に足し合わせる」という発想は教科書にも書いてありますから、何でもない事のように思われるかもしれませんが、コロンブスの卵と一緒で最初にこれを考えた人はやはり、偉大だと思うのです。そして、その偉大さに「賢いな~」と感動できる感性を持つ事が「地図と磁石」を手に入れる第一歩です。
