私の経験上、勉強の仕方に悩む生徒の多くは、公式を、解法を丸暗記することが勉強だと思っています。不幸なことにそう思わされてきてしまったのです。小学生のうちはそれでもある程度の点数は取れるでしょう。中学生でも要領がよければ、何とかついていくことができるかもしれません。しかし、高校生になってきますと、それでは通用しなくなってしまうのです。学年が進むにつれて、勉強の内容は飛躍的に難しくなり、その量も膨大になります。それらを丸暗記するのは大変な労力です。しかもその努力が成績に繋がらないとなれば、当然勉強は面白くなくなります。
ではどうしたら良いのでしょう？努力が報われて、すればするほど勉強が楽しくなるようなそんな夢のような勉強方法があるでしょうか…？
あります！それはズバリ、「覚えない」ことです。勇気を持って「丸暗記勉強法」の呪縛から脱出するのです！！

実際に教えていると、公式の弊害をよく感じます。生徒たちの多くは教科書や参考書に「公式」としてのっているものに、問題で与えられた文字なり数字なりを「あてはめる」だけの作業に終始してしまうのです。これはとても窮屈なことですね。例えるなら野球でフォームを決められれてしまうことに似ていると思います。イチローのように振り子打法で打ちたいのに、一本足で打つこと強要されてしまうような窮屈さです。
公式で大事なのは結果ではなく、プロセスつまり、そこに至る考え方です。先ほどの野球の例で言えば、ボールをバットの芯で捉えようとすること、それだけが重要であり、そのための「フォーム」は人によって違っていてもちろん構わないのです。公式のウラにあるプロセスには、4000年以上の数学の歴史における人類の叡智の結晶がつまっています。プロセスを学べば、その考え方を使う問題の多いことに気がつくでしょう。それは大学入試問題を作っている教員たちもそのプロセスに感動をして勉強をしてきた人たちだからです。
公式証明のプロセスは どんな問題よりも「最頻出問題」であると言っても過言ではありません。

公式のプロセスににこめられた過去の天才たちによる叡智の結晶を手に入れる方法を書きます。まず過去の偉人たちの手法を真似て、公式を証明することから始めます。この時は教科書なり参考書を見ながら、全く同じように模倣してください。と同時にそのプロセスにある「叡智」に素直に感動できる感性を磨いていきます。人間とは本当に賢いのだなあという事に感動をしながら筆をすすめていってください。その感動は、自分のしていることが「勉強」であることを忘れさせてくれるでしょう。
次は白紙に自分だけの力で公式の証明を再現します。この段階では自分もその叡智に一歩近づけたような気持ちになれてどんどん楽しくなってくるはずです。

これを続けているうちに、学問に取り組む時の正しい姿勢が自ずとついてきます。この勉強方法は過去の天才たちを「先生」にしているのと同じですから当たり前のことです。そしてこの「正しい姿勢」こそが勉強における最大の財産になります。

問題を解くという行為は、一人森の中に残され、そこからゴールを目指す事に似ています。その森が幸運にも以前来た事のある森ならばゴールまでの道筋を覚えている事もあるかもしれません。しかし、多くの場合はその森は初めて迷い込んだ森であり、そんな時、過去の「記憶」は頼りになりません。けれども、もし迷ったその人が地図と磁石を持つならば、どのような森であってもその２つを駆使してきっとゴールにたどり着くことができるでしょう。
勉強において「地図と磁石」を持てる人間は、新しい問題にあたった時に第一歩を自信をもって正しい方向に踏み出すことができます。テストで問題用紙をめくる時、以前やったことのある問題であることを祈るより、この「地図と磁石」を持てるようになることを目指す方がずっとずっと本質的でそして楽しいとは思いませんか？
では、具体的には「地図と磁石」とはどのようなものでしょうか？
ここに簡単な例を一つ出します。

もちろん地道に計算をしてもすぐに答えは出ます。中には答えを暗記している人もいるかも知れません。等差数列の和の公式を覚えていて
$$ \frac{（初項＋末項） \times 項数 }{2}= \frac{(1+10) \times 10}{2}=55$$
と計算した人もいるでしょう。しかし、このどれもがこの場合の「地図と磁石」ではないのです。　この場合の「地図と磁石」は、

 

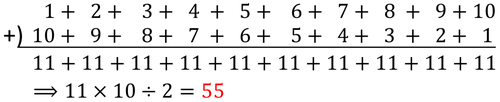
のように、考えることです。
これを少し進めて考えれば先の「等差数列の和の公式」へとすぐにたどり着きます。
この「地図と磁石」を持たないで、ただ公式として「等差数列の和の公式」を丸暗記している（していた）人は、少し応用問題を出されただけで途端にできなくなってしまったり、そもそも公式そのものを間違って覚えてしまっていたり、あるいはすっかり忘れてしまっていたりする事が少なくありません。しかし、この「地図と磁石」を持っている人は、この考え方を使って解ける問題の多いことに驚くでしょうし、公式はもはや知識ではなく知恵として一生忘れない財産になります。
まさにここに「地図と磁石」を手に入れるためのヒントとその醍醐味があります。
上の例で「逆に並べて上下に足し合わせる」という発想は教科書にも書いてありますから、何でもない事のように思われるかもしれませんが、コロンブスの卵と一緒で最初にこれを考えた人はやはり、偉大だと思うのです。そして、その偉大さに「賢いな～」と感動できる感性を持つ事が「地図と磁石」を手に入れる第一歩です。

公式のプロセスの模倣から始める勉強と公式の結果を丸暗記する勉強とは一体何が違うのでしょう？まず言えることは、前者は知恵であり、後者は知識であるということです。そして、その違いを生んでいるのが感動の有無です。誰にでも経験のあることだと思いますが、一夜漬けでつめこんだ「知識」はすぐに忘れてしまいます。しかし、感動という感性の働きを伴って自ら経験をしてきたことによって身についた知恵は決して忘れることはありません。
例を出しましょう。例えば年号です。「1192年　鎌倉幕府成立」というのをただ丸暗記している人がいるでしょうか？みんな、「いいくに（1192）作ろう鎌倉幕府」という有名が語呂合わせで覚えていますよね？そして他の年号は忘れても、おそらくこれは死ぬまで忘れることはない気がしませんか？ 何故でしょうか？それは語呂合わせをすることによって、単なる数字の羅列であった「1192」が「いい国作ろう」という「鎌倉幕府成立」のイメージ繋がる「物語」になっているからなんです。そににはある種の納得があり、「うまいこと考えたな～」という感動もあるでしょう。だから、この納得と感動を経験した人にとって「いいくに作ろう鎌倉幕府」は「知識」ではありません。 その人の頭と心に深く刻まれた「知恵」なのです。
私の言う「覚えるな」という言葉の真意もまさにここにあります。 丸暗記、覚えることで身につく「知識」なんて、どうせすぐ忘れてしまいます。 そんなもののために貴重な青春時代の多くの時間を割くなんて、何ともったいないことでしょう。覚えることをやめた時、人は己の「知恵」だけが頼りになるのです。
勇気を持って「丸暗記勉強法」の呪縛から脱出しましょう！！

知識ではなく知恵を蓄えようと説きました。 「知恵」が貯まっていくと人は自ら考える力、すなわち「独創」する力を育てることができます。公式のプロセスを模倣することで天才に近づこう、と書きました。偉大な先人たちを「模倣」することで身についた「知恵」は「独創」への扉を開いてくれます。プロセスを模倣することで、学問への正しい姿勢を身につけることができてくると、何を模倣するべきか、何を独創することができるかが判断できるようになります。そして学校で覚えなくてはならないとされている多くの事のほとんどを自ら紡ぎだせるようになります。

丸暗記を極力避けてとにかく「覚えない」こと、知識ではなく知恵を身につけるための努力に集中すること。 そして、独創できる人間を目指すこと。これが本当に大事なのです。

これを読んでいる高校生、受験生のあなたは勉強を楽しい！と思っているでしょうか？おそらく（大変残念ながら）「つまらない」と感じているのではないでしょうか？それは何故でしょう？
例えば、あなたが参考書なり、問題集なりにチャレンジしたとします。そんなとき問題が解けない（分からない）→解答を見る→解答を覚える、というプロセスに終始してしまってはいないでしょうか？つまり、一度やって出来なかった問題が二度目には出来るようにその解答を覚えることを「勉強」だと思ってはいないでしょうか？実はそれが勉強をつまらなくしてしまう最大の原因です！なぜなら、そうやって苦労して解法を覚えた問題は、もう二度と試験の本番で出会うことはないからです！そう、甲斐がないのです。努力が報われないから、やっていてつまらないのです。
ではどうしたら良いでしょう？答えは簡単です。やっても報われない努力はやめることです。覚えなければ良いのです。出来なかった問題の解法（解答）を覚えるのは無意味であることを知りましょう。今すぐ、考え方を変えて、これから出会う未知の問題が解けるようになるためにするべき勉強に切り替えましょう。出来なかった問題の復習は次のようにします。まず、解答の１行目に注目しましょう。それは、あなたが最初にチャレンジした時に出てきましたか？もし解答の１行目があなたと同じなら、あなたはその問題が解けるレベルのすぐ近くまで来ています。自信をもってくれていいです。２行目、３行目と丁寧に解答を読んでどこが自分と違うか、どこが自分では出すことが出来なかったのかを検証しましょう。そして、１行目が自分と全然違ったあなた、その最初の１行を出すためにはどんな考え方が必要だったかを 想像しましょう。それは思いもよらない発想でしたか？
それとも、公式の証明のプロセスで出会ったことのある発想ですか？ いずれにしても、その「発想」こそが最も学ぶべきところです。 出来なかった問題を解くために必要な「発想」が何であるか、そして、それを自分の力で出すためにはどんな捉え方が必要なのか、をじっくり自分に問いかけるように考えてみてください。その答えが出たとき、あなたはすでにその発想を手に入れていると言っても過言ではありません。
この勉強方法を続けていると、あなたは問題を解くために最も必要な発想、つまり「地図と磁石」を手に入れることができるでしょう。そして、それはあなたがテストで未知の問題に出会ったときに、最大限の力を発揮してくれます。 もちろん点数も自ずとついてくるでしょう。そうなれば、気がつけば、勉強が楽しくなっている こと間違いなしです。

私が受験勉強をしている頃、友達に「勉強が楽しい」と言うと、大抵変人扱いされました。もちろん、私は自慢や嫌味で言っているわけではなく、心から「楽しい」と思っていたのです。そして、東大に入ってから同級生と話していると「勉強が楽しい」と考えている人がとても多い事に気づきました。そう、諺にもあります通り、やはり「好きこそものの上手なれ」なのです。ではどうすれば、「好き」になれるのか。それはズバリ、「感性を磨く」事です。 例えばあなたが音楽をこよなく愛しているとします。そのあなたと、普段音楽に関心のないあなたの友人とが同じ音楽を耳にした時、二人は同じように「感じる」ことができるでしょうか？おそらく答えはＮＯです。なぜなら、あなたは毎日多くの時間を割いて音楽を聞いています。色々な音楽を聴いていることでしょう。そうすることであなたの音楽への感性は知らず知らずの内に磨かれているのです。だからあなたの友人には感じ取れなかったその音楽の素晴らしさにあなたは感動する事ができたのです！そう、実はこれは勉強でも同じです。丸暗記勉強法では決して得ることの出来ない感動を公式の証明に日ごろから多く触れることで得ることができるようになります。前にも書きましたとおり、最初は模倣で良いのです。そしてその「証明」がこの世に存在しなかったときに、それをこの世に誕生させることの困難と奇跡にどうぞ想いを馳せてください。想像してみてください。それを最初に発見した人が手にしたであろう感動、それを最初に聞いた人々が得たであろう感動を。そして、あなたは気づくでしょう。人間の叡智の素晴らしさに感動している自分自身に。
こう考えてくると勉強が好きになる方法は意外と簡単ですね。

というわけです。
勉強＝「勉めて強いられる」もの、という言葉が良くないのかもしれないですね。 その「勉強」が楽しくなるために、どうぞ自分から進んで取り組んでみてください。人から言われて嫌々やっている内はどう転んでも勉強は楽しくないし、楽しくない勉強は効率が悪く、ストレスばかりが溜まり、成績も伸び悩みます。
そしてますます勉強が楽しくなくなります。多くの学生がはまる悪循環です。どうぞ忘れないでください。あなたの時間はあなたのためにあります。能動的な勉強の第一歩は、進んで公式の証明に取り組むことです。

教育とは…
学校で教わったことを全て忘れた後にのこるものだ。

 

---

ある真実を教える事よりも、
真実を見出すにはどうしなければならないかを
教える事の方が重要である

 

---

子供は誰でも芸術家だ。
問題は、大人になっても
芸術家でいられるかどうかだ。

 

---

塩の辛さ、砂糖の甘さは学問では理解できないが、
なめてみればすぐ分かる。

 

---

人を教えることはできない、
ただ自悟させる手助けをするにすぎない。

 

---

平凡な教師は言って聞かせる。
よい教師は説明する。
優秀な教師はやってみせる。
しかし最高の教師は子どもの心に火をつける。